Author: Aurimas
-
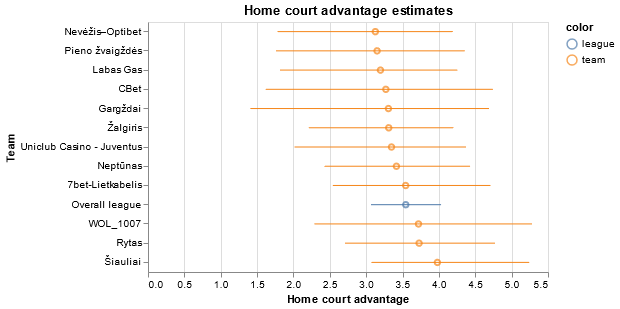
Estimating home court advantage in Lithuanian Basketball League with Gaussian Processes
I was looking for an excuse to play around with Gaussian Processes in a Bayesian Inference setting, and decided to revisit an older project about basketball in Lithuania. Just in time for this year’s finals!
-
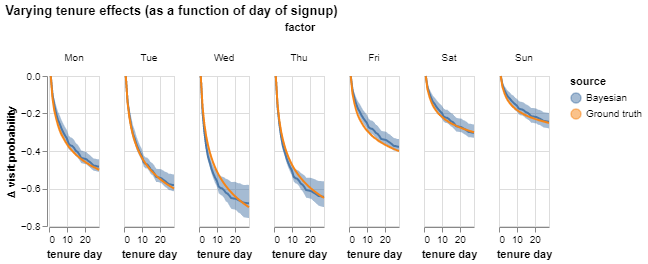
Modeling tenure effects the Bayesian way
After learning new things in Statistical Rethinking class, I took on to play around with an age-period-cohort-like model for disentangling tenure effects from seasonality & other factors. The Bayesian way.
-
Getting faster to decisions in A/B tests – part 2: misinterpretations and practical challenges of classical hypothesis testing
Null hypothesis test of means is the most basic statistical procedure used in A/B testing. But the concepts built into it are not exactly intuitive. I go through 5 practical issues that anyone working with experimentation in business should be aware of.
-
Getting to decisions faster in A/B tests – part 1: literature review
I set out on a journey to learn what statistical approaches the industry uses to get to faster decisions in A/B testing. This is the first post in the series in which I set the scene and summarize outcomes of my “literature review”.
-
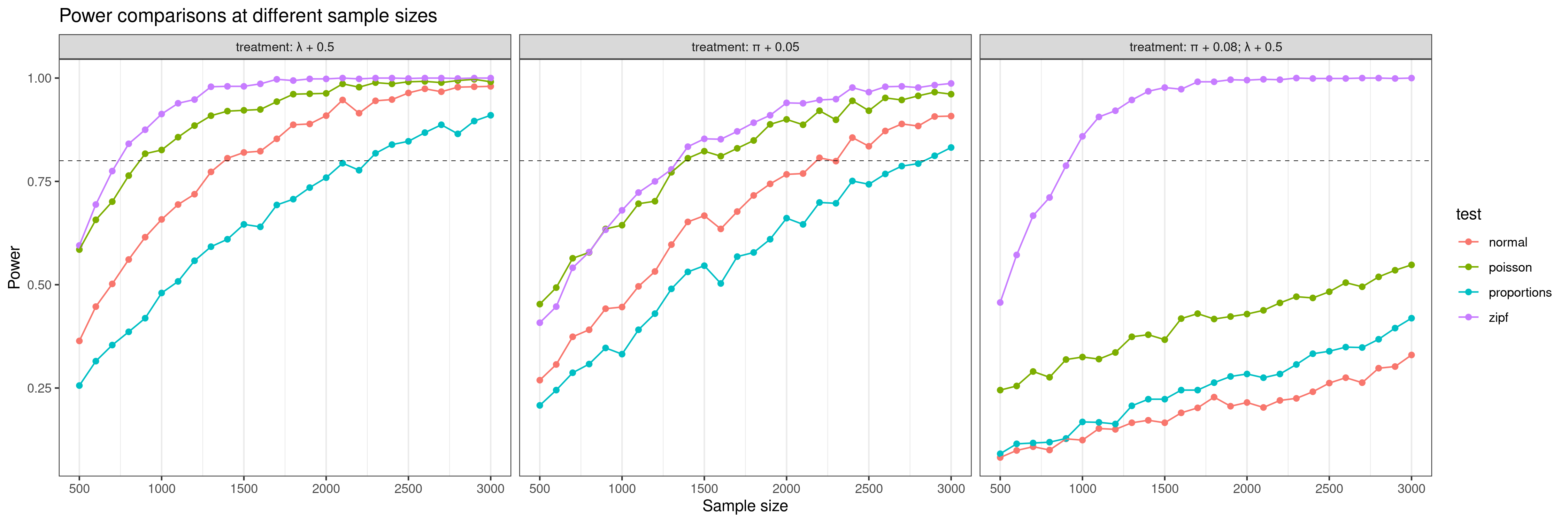
A/B testing, zero-inflated (truncated) distributions and power
Naive A/B testing just uses t-tests or proportion tests, with the assumption that at large sample sizes, the right statistical test does not matter that much. I explore the case of a zero-inflated upper-bounded Poisson distribution and find that using the wrong test can require 3x the sample size to achieve the same statistical power,…
-
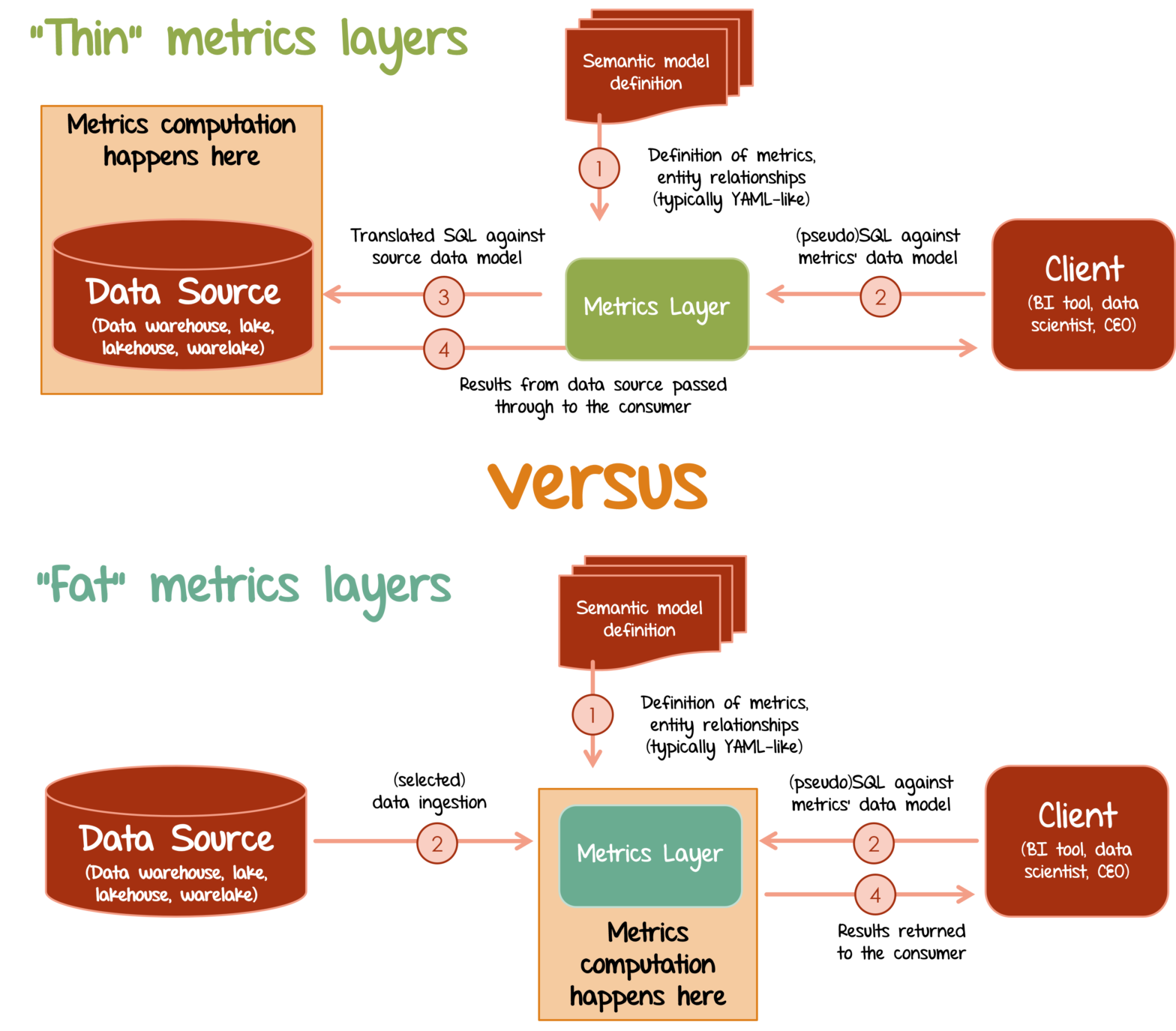
The Jungle of Metrics Layers and its Invisible Elephant
Metrics layer is the rising “missing component” of the modern data stack. I dive into functionalities provided by 10 prominent players in the space and contrast them with a player no one talks about: Microsoft Power BI.
-
Grappling with privilege
Realizing you’re privileged is uncomfortable. It’s like understanding you can have a cake and eat it, too, except you never asked for the damn cake and you now realize most people aren’t as lucky as you are.
-
Gaussian Processes: a versatile data science method that packs infinite dimensions
Last semester, I learned about Gaussian Processes. They seemed really intriguing at the first glance, and it turned out they are even more intriguing as you dig deeper. This post is an application-oriented intro to Gaussian Processes. I’ll cover GP regressions, forecasting for time series and usage of GPs in bayesian optimization among other things.
-
An interactive introduction to wavelets and discrete wavelet transformation for data scientists
I built a practical intro guide to wavelets and discrete wavelet transformation for data scientists. Welcome to magic!
-
Interpretation of log transformations in linear models: just how accurate is it?
Log-transformations and their interpretation as percentage impact is taught in every introductory regression class. But are most people aware that there is a hidden approximation behind the percentage-based intuition? One that may not be appropriate in some cases?